cs50 4강 검색 알고리즘

들어가기에 앞서

위 파트는 챕터4인 알고리즘 파트의 세션 1-3까지만 정리한 글입니다.
검색 알고리즘에 대해 다루는 게시물 하나, 정렬 알고리즘 게시물(6세션 까지),나머지 재귀와 병합정렬 게시물 하나로 총 3개의 게시물로 정리할 예정입니다.

검색 알고리즘

여기에서 말하는 검색 알고리즘이란 배열을 검사할 때 어떻게 하면 인덱스를 효율적으로 접근할 수 있느냐에 대한 고민이나 마찬가지이다.
1세션에서는 검색을 하는 방식에 따라 선형 검색과 이진 검색으로 구분지어 설명을 하고있다.

선형 검색

배열을 처음부터 끝까지 탐색하는 방식이다.
이러한 탐색은 입력의 순서에 대해 보장해야하는 경우(원본 배열을 해치면 안되는 경우),정렬이 안되어있는 경우 유용하게 사용할 수 있다.
단순하게 코드를 짜보자면 for문을 통해 전체를 순회하고 내가 원하는 상황이 되면 종료한다고 생각하면 된다.

for(int i=0;i<arr.size();i++){
  //전체 탐색중
  if(내가 필요한 상황이 되면){
    //원하는 작업 시행
    return 0;
  }
}

이진 검색

만약 배열이 정리가 되어있거나, 원본 배열의 순서보다는 값의 대소가 상관이 있는 상황이라면 정렬을 한 뒤에 사용하면 유용한 탐색방법이다.
배열의 중간부터 시작해서, 자신이 찾고자 하는 값과의 대소를 비교하여 인덱스를 이동시키는 방식이다.

c++에서 이진 검색

역시 없는 것을 찾는 게 더 빠른 c++답게 이진 검색도 stl로 제공하여준다.
사용방법은 다음과 같다.

#include<algorithm>
binary_serach(시작주소,시작주소+배열크기,찾기를 원하는 값)

위의 코드를 입력하면 리턴값이 존재한다면 1 없으면 0으로 자동으로 값을 반환해준다.

알고리즘 표기법

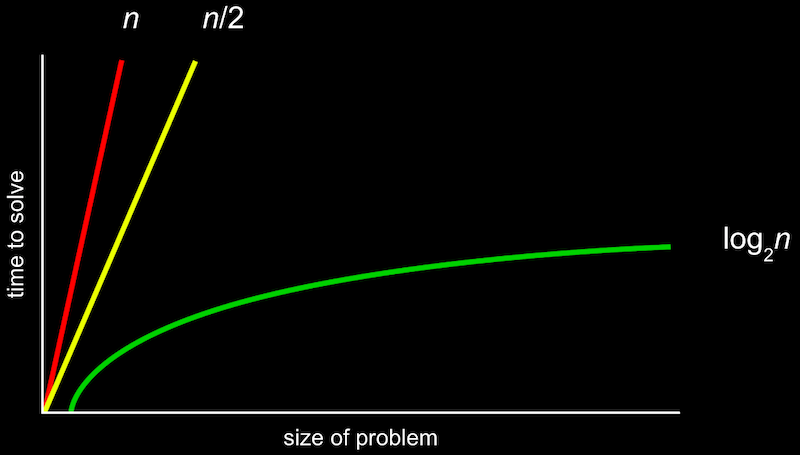
위 이미지는 정렬 알고리즘은 Big O로 표기한 것이다.
여기에서 중요한 것은 Big O는 알고리즘의 실행시간의 상한선 즉 최악의 경우를 가리키기 때문에, 운이 좋다면 표기된 시간보다 빠르게 답을 도출해낼 수 있다.

소요시간 대소관계

O(1) < O(log n) < O(n) < O(n log n) < O(n^2)

여기에서 O(1)은 입력의 크기에 상관없이 일정한 시간을 소요하는 작업들 이야기한다.
queue의 front를 가져오는 작업과 같이 크기에 상관없이 같은 시간을 소유하는 작업들의 시간복잡도를 상수 시간 복잡도 라고도 부른다.

Big Ω

이것은 알고리즘 실행시간의 하한선 즉 운이 좋은 경우에 대해 나타낸다.
따라서 크기가 작은 경우나, 시간이 크게 구애받지 않는 경우 Big Ω을 기준으로 생각해도 괜찮다.
그러나 알고리즘 문제 풀이와 같이 실행시간에 따라 정답이 나뉠 수 있는 경우 Big O를 기준으로 생각하는 것이 정신에 이롭다.

선형 검색

선형 검색은 원하는 자료가 나올 때까지 앞에서부터 끝까지 검색하는 방식이다.
따라서 정확도는 높지만, 이게 뭔 알고리즘이야라는 생각이 들만큼 비효율적이다.
대신 자료를 정렬하면 안되는 상황인데, 주어진 조건이 하나도 없어서 하나하나 자료를 뒤져야하는 상황에서는 나름 유용하다.
랜덤으로 탐색을 하는 것보다는, 선형 검색을 하게 되면 자료를 앞에서부터 뒤지니 정확할 뿐 아니라 운이 좋다면 빠르게 값을 찾아낼 수 있기 때문이다.

구조체

구조체는 일종의 자료형을 내가 마음대로 만들어내는 것이다.
그래서 내가 필요한 어떤 자료나 기준들을 만들 수 있을 뿐 아니라, 거기에서부터 파생되는 기능들을 만들 때에 유리해진다.

예시

안타깝게도 내가 전에 만든 예시를 재탕한 자료여서 c++로 만들어진 코드이다.
그러나 구조체의 용도에 대해서는 감을 잡을 수 있을 것 같아 첨부를 하였다.

class Queue {
private:
    struct Node {
        int data;
        struct Node* next_Node;
    };

    Node* frontNode;
    Node* backNode;

public:
    Queue() : frontNode(nullptr), backNode(nullptr) {}
       void push(int data) {
        Node* newNode = new Node;
        newNode->data = data;
        newNode->next_Node = nullptr;
        if (isEmpty()) {
            frontNode = backNode = newNode;
        }
        else {
            backNode->next_Node = newNode;
            backNode = newNode;
        }
    }
    //이하 생략...
};